「カイ二乗分布ってどういう分布なの?」
「どのような使い道があるの?」
「エクセルやカイ二乗分布表で実際に確率を求めたい」
このような疑問や悩みをお持ちの方に向けた記事です。
カイ二乗分布とは、標準正規分布$N(0,1)$を基にした確率変数の二乗和が従う確率分布のことです。
「カイ二乗」という名前からして難しそうで敬遠しがちですが、統計学の上では検定や推定、適合度の検定などを行う上で欠かせない基礎知識の一つです。
この記事では、カイ二乗分布の定義と性質、活用の用途、期待値と分散の導出の仕方、エクセルやカイ二乗分布表から確率を求める手順について解説しています。
初心者の方にもわかりやすいよう、できるだけ細かく手順を踏んで説明しますので、参考になればうれしいです。
カイ二乗分布とは?
定義
最初にカイ二乗分布の定義を説明しておきます。
「カイ」は記号で「$χ$」と表され、以下の数式によって定義されます。
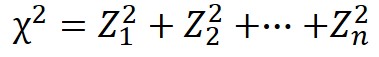
ここで、$Z_{1}~Z_{n}$は標準正規分布に従う互いに独立な確率変数を表します。
標準正規分布とは、正規分布において平均値$μ$を0、標準偏差$σ$を1として基準化したもので、$N(μ,σ^{2})$は$N(0,1)$と表記されます。
この$χ^{2}$が従う確率分布のことをカイ二乗分布と呼び、自由度$n$のカイ二乗分布に従うと表現されるのです。
※ちなみに、この記事では自由度を$n$と表記していますが、QC検定の問題のようにサンプルサイズと自由度が両方登場する場合には、サンプルサイズを$n$、自由度を$φ=n-1$と記載することもあります。
確率密度関数
カイ二乗分布の確率密度関数は以下の数式で定義されます。
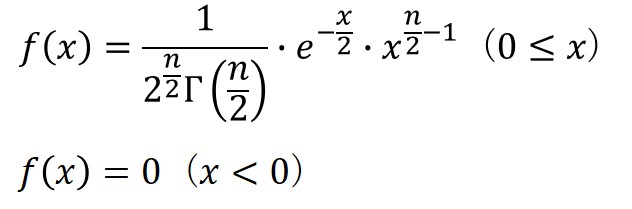
$e$は自然対数の底、$n$は自由度、$Γ()$はガンマ関数を意味します。
ガンマ関数とは、階乗の概念を表す特殊な関数で、$Γ(n)=(n-1)!$として定義されます。

数式が複雑すぎてサッパリ・・
数式が非常に難解ですが安心してください、覚える必要はありません。
後ほど説明するエクセルの関数やカイ二乗分布表を用いれば、複雑な計算式を解かなくても、簡単に確率を求めることができます。
なお、標準正規分布や確率密度関数については、別の記事で詳しく紹介していますので、合わせて参考にしていただければと思います。


カイ二乗分布の性質
カイ二乗分布に関する主な性質を3つ紹介します。
1.和に関する再生性
確率変数$Z_{1}, Z_{2}$がそれぞれ独立に自由度$n_{1}, n_{2}$のカイ二乗分布に従うとき、確率変数の和$Z_{1}+Z_{2}$もカイ二乗分布に従い、その自由度は$n_{1}+n_{2}$となります。
この性質を和に関する再生性と呼びます。
2.母分散と不偏分散の関係
確率変数$Z_{1}, Z_{2}, ・・・, Z_{n}$が正規分布$N(μ,σ^{2})$に従うとき、母分散と不偏分散から以下の数式で求められる$Y$は、自由度$n-1$のカイ二乗分布に従います。

この式を見ても分かる通り、カイ二乗分布は母分散と不偏分散の比を表しているだけと考えれば、それほど難しく感じないですね。
母分散と不偏分散については、別の記事で詳しく紹介していますので、合わせてご覧ください。

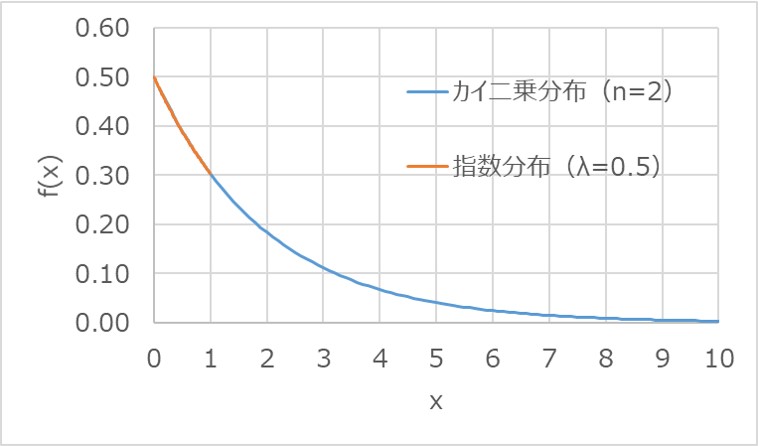
3.自由度2のカイ二乗分布は指数分布
自由度2のカイ二乗分布は、$λ=0.5$の指数分布と一致します。


活用の用途
ここまで、カイ二乗分布の定義と性質について説明しましたが、いったい何に使えるのか?実用例のイメージが付きにくかったかもしれません。
カイ二乗分布は、確率変数の二乗和が従う分布なので、すなわち、「ばらつき」「分散」に関わる確率を求める場合に活用されます。
ここでは、カイ二乗分布の主な3つの使い道について説明します。
1.独立性の検定
独立性の検定とは、2つ以上の変数において、変数どうしの差があるのか調べるための検定手法です。
例えば、2つの製造ラインの不良項目の内訳に関して、以下のようなクロス集計表のデータがあったとします。

不良の発生割合に製造ライン間の差があるのか、カイ二乗分布を用いれば調べることができるのです。
独立であるか(関連性がない)、否か(関連性がある)、2つの製造ラインに対して、それぞれ平均値に対する「ばらつき」を比較することで、関連性の有無を統計的に求められます。
2.適合度の検定
独立性の検定と似た手法として、適合度の検定があります。
2つの変数の比較ではなく、あらかじめ構成比率の理論値が分かっている場合において、集計結果が理論値と適合するか、否かを調べるための検定手法です。
独立性の検定と同様に、カイ二乗分布を用いて理論値との差に対する「ばらつき」を見ることで、適合の有無を見ることができます。
3.母分散の検定と推定
母分散の検定とは、ある標本調査の結果から得られた分散の値が、母分散の値と等しいか、否かを調べるための検定手法のことです。
また、母分散の推定とは、ある標本調査の結果から得られた分散の値から、母分散の範囲(信頼区間)を推定する手法のことです。
どちらも分散に関する確率として、カイ二乗分布が適用されます。

カイ二乗値の二乗和も分散と同じ考え方だったね
期待値と分散の導出
カイ二乗分布における期待値$E(X)$と分散$V(X)$は、以下となります。
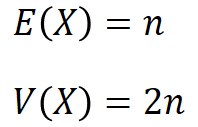
導出過程に興味のある方は参考にどうぞ。


なお、$E(X)$と$V(X)$の意味、$V(X)$の導出の過程については、別の記事で解説していますので、合わせてご覧ください。

エクセルでのグラフの書き方
エクセルでのカイ二乗分布の確率の求め方、グラフの書き方を紹介します。
CHISQ.DIST関数を用いれば、確率密度関数を計算することができます。
DISTというのは、分布(distribution)の略で、CHISQはカイ二乗を表すchi-squareの略で、これを繋げた名前が関数名になっています。
使い方は簡単で、次の3つの変数を指定するだけです。
①:カイ二乗値($x$)
②:自由度($n$)
③:関数形式(TRUE or FALSE)
③の関数形式については、確率密度関数を求めたい場合はFALSE、累積分布関数を求めたい場合はTRUEを選択しましょう。
累積分布関数とは、確率変数がある値以下となる確率の関数のことで、以下の数式で定義されます。
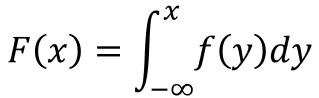
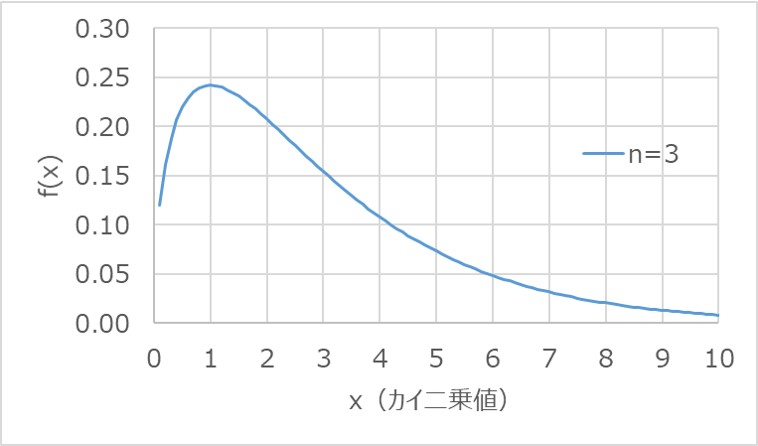
例えば、自由度$n=3$として、確率密度関数$f(x)$を求めると以下のようになります。
また、同様に累積分布関数$F(x)$を求めると以下になります。
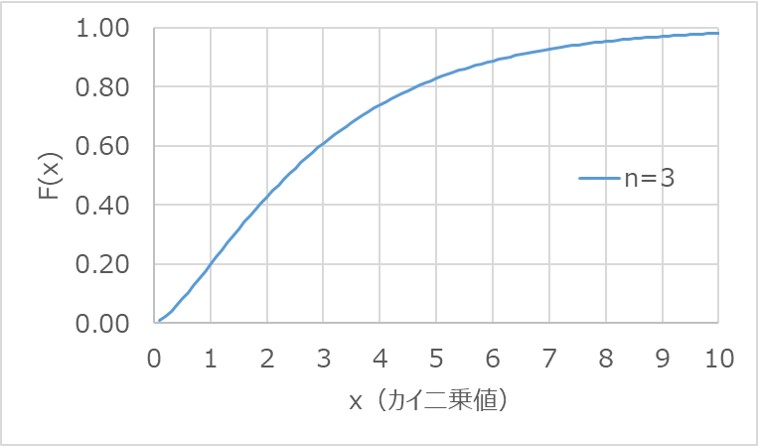
累積分布関数は、確率変数$x$の値が大きくなるにつれて、1に収束することが見て取れます。
これは、確率の合計値が1になることを表しており、この性質がグラフからも分かります。
なお、エクセル関数にはCHISQ.DIST.RT関数と呼ばれるものもあります。
累積分布関数$F(x)$は、確率変数がある値以下として定義されますが、CHISQ.DIST.RT関数はある値以上の確率を表しており、つまり、以下の数式をこの関数で直接計算できるのです。

これは、カイ二乗分布を用いた検定や推定を行う際に、カイ二乗値がある値以上になる確率を求める場合も多いため、関数として用意されている訳です。

実用的だから覚えておこう
カイ二乗分布のグラフの特徴
右側に裾広がりの形状を示す
カイ二乗分布のグラフは左右対称ではなく、右側に裾広がりの形状を示します。
以下のグラフは、自由度の違いによる確率密度関数の形状の違いを表したものです。
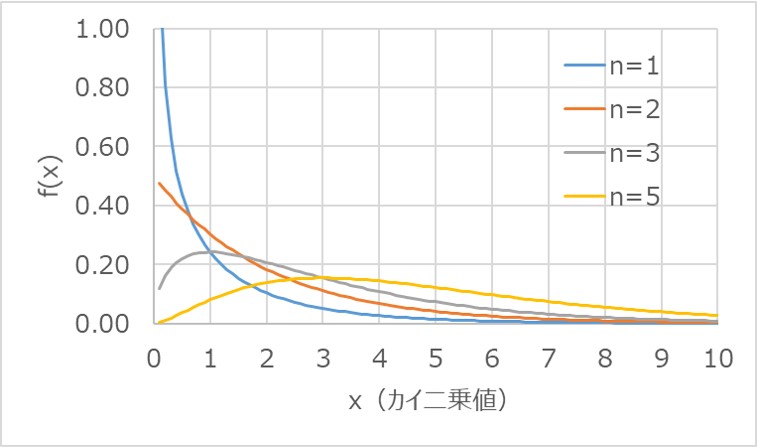
いずれも、右側に広がった分布を示していることが分かります。
また、自由度の増加にともない、ピークの中心が右側にシフトしていきます。
無限大で正規分布に収束する
カイ二乗分布の自由度を大きくして極限を取ると、正規分布に近似できます。
特に、カイ二乗値を以下の数式により標準化して極限を取ると、標準正規分布$N(0,1)$に近似することができます。
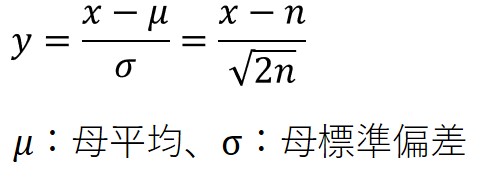
以下は、自由度$n=50$におけるカイ二乗値を標準化した分布と、標準正規分布をプロットしたグラフです。
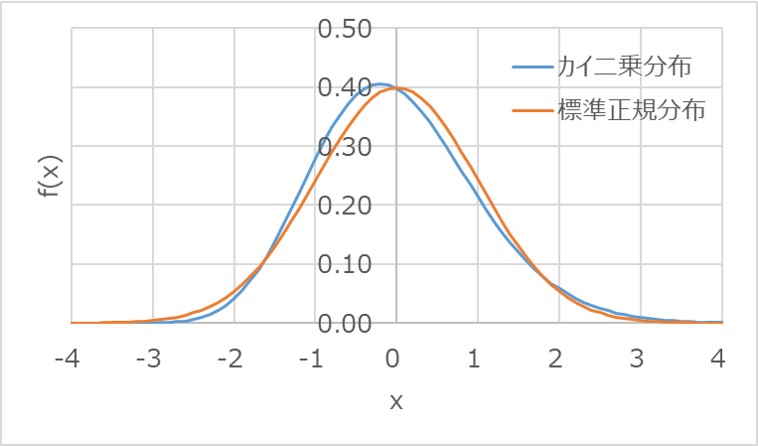
標準正規分布は0を軸として左右対称ですが、カイ二乗分布の方では、ややピークが左寄りの形状が残っています。
ただ、全体的な分布形状としてはほぼ一致しており、自由度が十分に大きい場合には正規分布として扱って問題ないことがグラフを見ても理解いただけるかと思います。
正規分布、標準正規分布については、別の記事で詳しく紹介していますので、合わせてご覧ください。

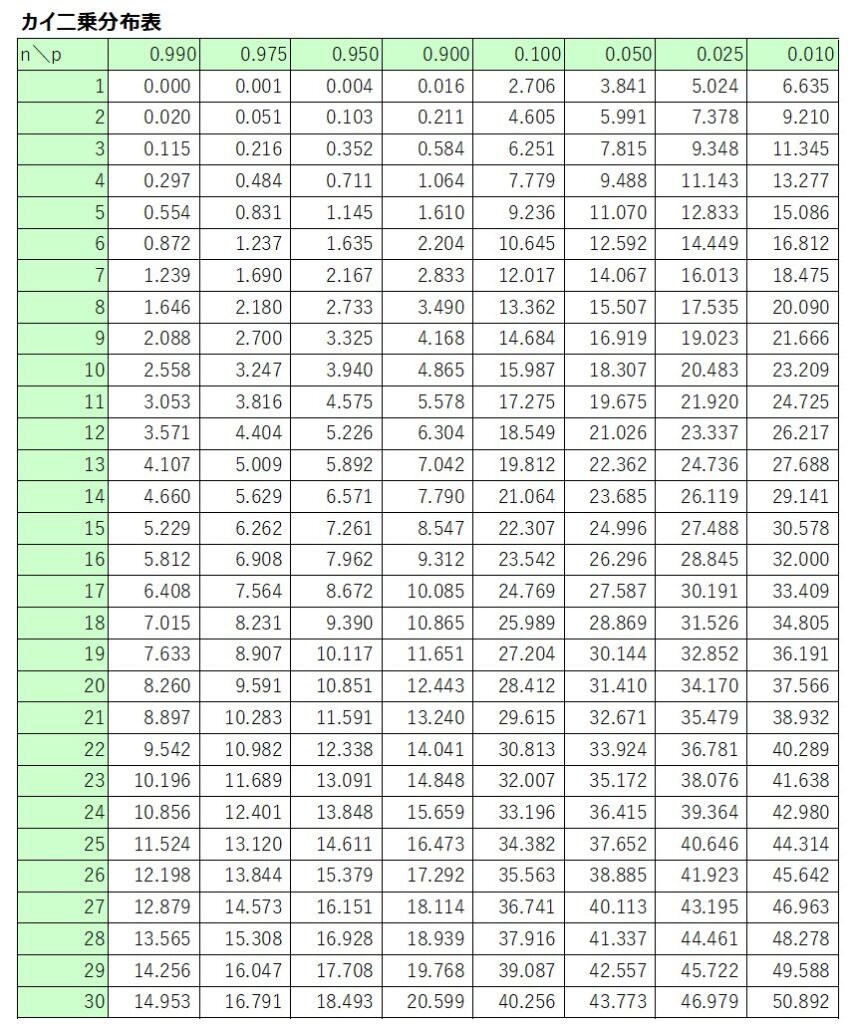
カイ二乗分布表の読み方
カイ二乗分布表とは、横軸に確率$p$、縦軸に自由度$n$を取って、マトリックスの交差する箇所に対応するカイ二乗値が記載されている表です。
ここで表す確率$p$は、カイ二乗値に対する右側(上側)確率を意味します。
つまり、カイ二乗値がとある値よりも大きくなる確率を表しています。
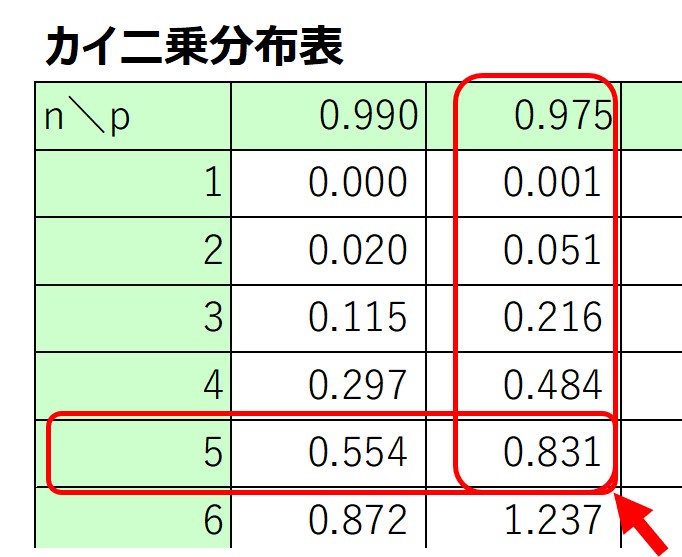
例えば、自由度$n=5$、右側確率$p=0.975$におけるカイ二乗値は$0.831$と読み取ることができます。
活用例の項目でも説明した各種の検定や推定を行う際に、カイ二乗分布表を用いれば、複雑な計算をすることなく、所望のカイ二乗値を得られるので大変便利です。
なお、エクセルを用いて自分でカイ二乗分布表を作る場合は、CHISQ.INV.RT関数を用いると簡単に計算することができます。
これは、カイ二乗分布の確率の逆関数を求めるもので、自由度と右側確率を指定すれば、対応するカイ二乗値を計算できるのです。

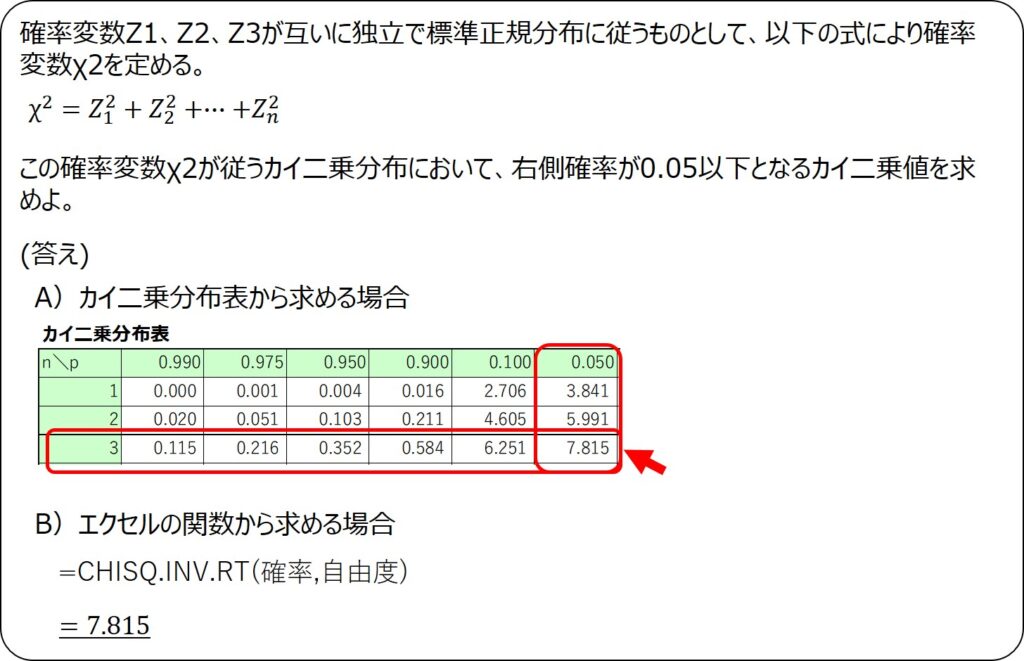
例題
まとめ
- カイ二乗分布
⇒標準正規分布$N(0,1)$を基にした確率変数の二乗和が従う確率分布 - 活用の用途
⇒独立性の検定
適合度の検定
母分散の検定と推定 - 期待値と分散
⇒期待値:$n$、分散:$2n$($n$は自由度を表す) - エクセルでの求め方
⇒CHISQ.DIST関数で、確率密度関数と累積分布関数を計算できる - カイ二乗分布のグラフの特徴
⇒右側に裾広がりの形状を示す
⇒無限大で正規分布に収束する - カイ二乗分布表
⇒横軸に右側確率$p$、縦軸に自由度$n$、マトリックスの交差する箇所にカイ二乗値が記載された表
使うタイミングさえ、きちんと覚えておけば、あとはエクセルやカイ二乗分布表から簡単に計算できます。
製造ばらつきの比較や推定など、品質管理の現場でも活用する場面は多いので、ぜひ使いこなせるようにしておきましょう。
最後まで読んでいただき、ありがとうございました。
この記事で紹介したカイ二乗分布は、統計的品質管理を実践する上での基本要素の一つです。
製造業に携わるエンジニアであれば、その他の統計的手法はもちろんのこと、品質管理、生産の基礎知識を幅広く身につけておく必要があります。
社内講座などの機会が設けられている場合は、ぜひ若手のうちから積極的に活用して受講することをおススメします。
ただ、多くの社員を対象とする社内講座の場合、皆さん一人ひとりのレベルに適した学習ができない場合もあります。
忙しい日々の限られた勉強の時間を最大限に活かすためにも、自分の教育プランは自分で管理することを意識して、能動的に学習することも検討してみてはいかがでしょうか。





コメント