QC検定(品質管理検定)2級の受検をお考えの皆さま必見です。
・受検を考えているけど、何から勉強すればいいの?
・分野ごとの出題の頻度は?
・どのような問題が出るのか傾向を知りたい
このような疑問や悩みをお持ちではありませんか。
仕事や日常生活の忙しい中で資格の勉強をするには、とにかく学習効率が重要です。
何となく机に向かい参考書を眺めているだけ、過去問や問題集の目の前の問題をただひたすら解いているだけでは、その時々の行き当たりばったりの勉強になってしまいます。
効率良く学習するには、まず出題分野の全体像を把握し、それぞれの分野でどのような特徴の問題が多く出題されるのか分析が必要です。
この記事では、QC検定2級の手法編の受検対策として、2級の出題分野、分野ごとの出題頻度、過去問から分析した問題の特徴を解説しています。
ぜひ、皆さんの参考になればうれしいです。
なお、3級の出題傾向については、別の記事で紹介していますので、3級の受検をお考えの方はぜひご覧ください。

2級の出題分野
QC検定2級の手法編の出題分野は、日本規格協会グループのサイトにもレベル表に記載されていますが、主だったところを整理すると次のようになります。
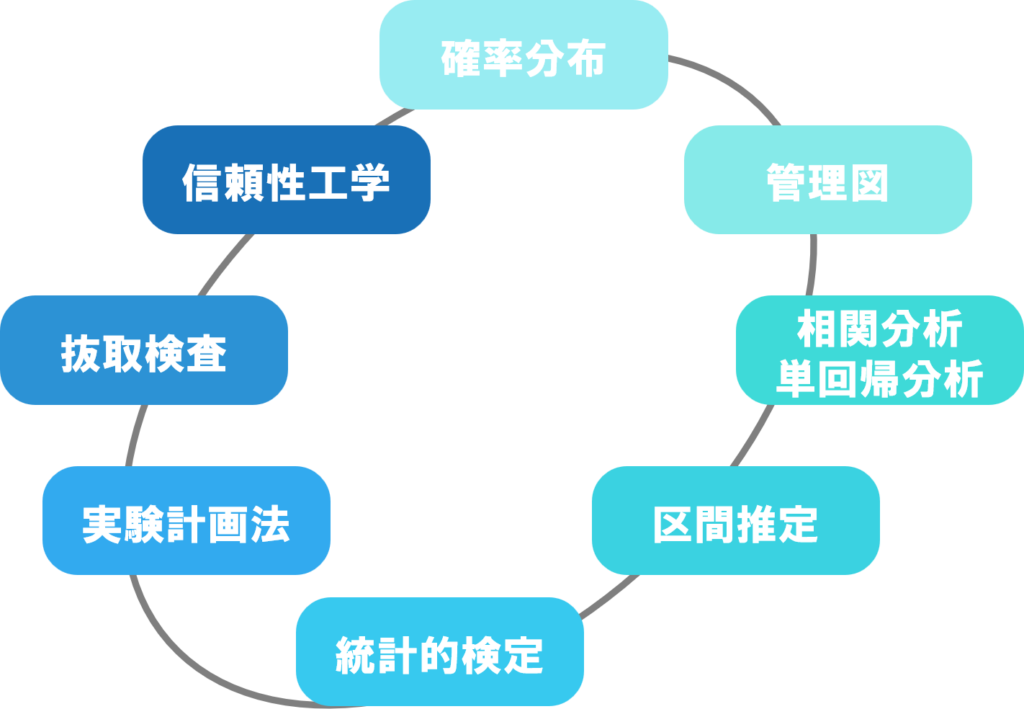
3級ではQC7つ道具を押さえておけば、試験分野のかなりの領域をカバーできていたのに対して、2級では驚くほど出題範囲が広くなります。
特に、統計的検定や区間推定、実験計画法は2級の代名詞とも言えるもので、この辺りから統計の計算に悩まされて、諦めてしまう方も少なくないのではと思います。
まずは頻出8分野の概要について紹介します。
確率分布
正規分布、二項分布、ポアソン分布が対象となっています。
このうち、正規分布と二項分布は3級でも登場する内容で、正直なところさほど難易度は変わらないので、3級を取得済みの方にはサービス問題と言えるかもしれません。
新たに登場するポアソン分布は、名前だけで難しそうな雰囲気に圧倒されそうですが、定義の式が与えられていることも多く、深い知識が必要なわけではありません。
管理図
QC7つ道具のひとつで、3級でも多く出題される分野の一つです。
2級では他のQC7つ道具はほぼ登場せず、管理図だけが特出しとして出題されます。
上下限の規格値と標準偏差から工程能力指数を計算したり、管理限界線の定義の式を選んだり、2級ならではの難易度になっているので、3級でやったからと油断しないようにしましょう。
相関分析/単回帰分析
一見、3級の散布図問題のようにも見えますが、相関係数や回帰式を求めたり、無相関の検定を行ったり、統計的手法での計算が必要となります。
また、回帰式の有意性を調べるための分散分析は、まさに2級特有の問題です。
区間推定
標本サンプルのデータから母集団の統計量を求める問題で、いよいよ分散の計算やKpの考え方の理解度が問われる内容となっています。
統計的検定とセットで登場することも多いので、合わせてマスターしておきましょう。
統計的検定
ずばり、2級の代表格と言える分野で、次に記載する実験計画法との2大巨頭と言っても過言ではないかと思います。
しかし、帰無仮説、有意水準、棄却・・・といったように、そもそも用語自体が聞きなじみのないものが多く、毛嫌いしているかたも多いのではと思います。
ただ、過去の出題頻度から見て避けては通れないので、2級を受検するからには諦めて基礎から習得する道を選びましょう。
実験計画法
検定と同じく、代表格の分野です。
分散分析表が強烈に難しそうな印象を植え付けていると思いますが、実はやっていることは機械的な計算で、手順を理解してしまえば、あとは電卓をひたすら打ち込むだけなのです。
抜取検査
もう、ここまででお腹いっぱいという方もおられるかもですが、頻出分野の紹介もあと一息です。
抜取検査というと、どういうことをやっているか、何となく想像は付くと思います。
ただ、JIS規格にもとづく抜取検査は、計数とか計量規準型とか、一回抜取や二回抜取といったように手法が決まっており、分類と名称の複雑なことが敷居を高くする要因かもしれません。
信頼性工学
最後は信頼性工学です。
いよいよ、一つの学問の分野まで登場して、膨大な知識量を必要とするイメージがありますが、2級で求められる知識は限られており、問題も一定パターンに収まるものが多いです。
分野ごとの出題頻度
ここで先ほどの出題分野に関して、2018年から2021年までの6回の試験での登場する頻度を見てみましょう。
次の表の丸印は、その分野の問題が出題されたことを表しています。
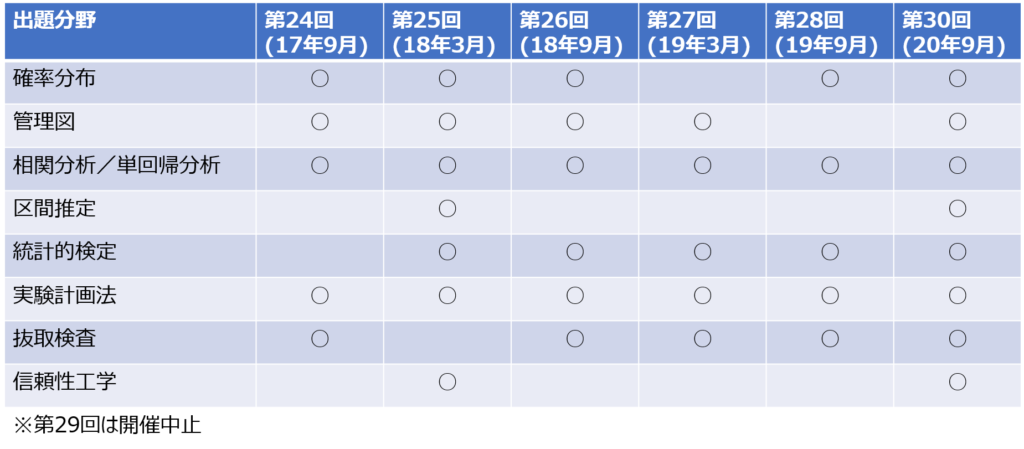
出題分野を大きく分類したこともありますが、ほぼすべて毎回に近いことがお分かりいただけると思います。
QC検定では合格基準の目安として、7割程度の正解率と言われており、各大問につき5~8問程度の小問が設定されています。
小問は手法編と実践編合わせて100問近くあるので、仮に8割正解を目指すとなると約80問の正解が必要となります。
つまり、苦手分野を丸ごと捨てたり、最初の小問で間違えたりすると、大ダメージを受けることになり、合格の可能性が大きく遠のいてしまいます。
試験本番で焦らず柔軟に対処できるようにするためにも、次に示す問題の特徴をきちんと押さえて、どのような形式で問われても苦手意識の残らないよう準備しておきましょう。
過去問の特徴
2018年から2021年までの過去問をもとに、私なりに特徴を分析してみました。
順番に一つずつ見ていきましょう。
確率分布
定義の式や文章に合致する名称を選ぶ問題
- 与えられた定義の式から確率を計算する問題
- 平均値と標準偏差から正規分布表の確率を読み取る問題
- 正規分布の確率に対応する平均値と標準偏差を求める問題
先ほどにも述べたように、正規分布と二項分布は3級からさほど難易度は変わりません。
正規分布では、与えられた平均値と標準偏差の値を標準化してKp値を求め、正規分布表から対応する確率を読み取る解法を知っていればバッチリです。
また、二項分布やポアソン分布で確率を求める問題に関しても、問題文に定義の式が与えられていることが多いので、あとは数値を当てはめれば答えを求められます。
以下の記事では注意点と模擬問題を解説していますので、合わせてご覧ください。

また、確率分布の基本から学びたいかたは、こちらもご覧ください。


管理図
- 管理限界線(UCL, LCL)を計算する問題
- 管理図を用いて工程の安定状態を判定する問題
- 目的別の管理図の定義に関する問題(解析用/管理用)
- 標準偏差と工程能力指数を求める問題
管理限界線や工程能力指数を求める問題は、3級でも出題されることがあるので、すでに習得済みの方も多いのではと思います。
2級では定義の式が問われることもあり、さらに実際に管理図を用いて工程の安定状態を判定する問題が出題され、求められる知識レベルが一段と上がります。
単に管理限界線の値を計算できるだけでなく、どういう目的で使用して、どのように活用すれば必要な管理ができるのか、実用性に関する理解度を問われているものと思います。


相関分析/単回帰分析
- データ表から相関係数を求める問題
- 相関の検定に関する問題
- 散布図に合致する相関係数の対応を選ぶ問題
- 相関係数、寄与率を求める問題
- 分散分析表を使って有意性を検定する問題
- 回帰式の定義を選ぶ、または回帰係数を求める問題
この辺りの分野からいよいよ本格的な統計の計算が必要になってきます。
ポイントとしてまずは、何といっても偏差平方和の考え方に慣れることです。
統計学の入り口として「ばらつき」に関する概念を持つことは必須です。
正直なところ、偏差平方和の計算式は空で言えるくらいになっていないと、正答率8割を目指すのは難しいかもしれません。
逆に言うと、偏差平方和を難なく求められるレベルになっていれば、その後の計算は簡単な四則演算で求められるものが多いので、最初のひと山を頑張って乗り越えましょう。
実際のところ、相関係数、無相関の検定統計量、分散分析、回帰係数など、いずれも偏差平方和さえ求められれば、あとは簡単に答えを導けます。




区間推定
- 信頼区間の計算式を選ぶ問題
- 信頼区間を計算する問題
区間推定で問われることは非常にシンプルで、まさに信頼区間を求めるための計算式を理解して正しく答えを導き出せるか、ということです。
区間推定の種類には、母平均、母平均の差、不適合品率・・・といったように多くの種類があり、覚えるのが大変なように思いますが、実は式の構造はほとんど同じなのです。
分散に関する区間推定は少し式の構造が違いますが、平均に関しては上表に示した通り、$K_{p}\sqrt{V/n}$の形で表されます。
これは母集団から抜き取った標本平均のばらつき(標準偏差)が何個分に該当するか、ということを意味しており、このように式の構造から理解すれば効率よく覚えられると思います。


統計的検定
- 帰無仮説または対立仮説を選ぶ問題
- 検定統計量を求める、または計算式を選ぶ問題
- 付表から棄却限界値を読み取って判定する問題
- 棄却・採択の結果から検定の結論を選ぶ問題
まさに統計的手法の代表格と言える分野ですが、問題の形式は案外と決まった流れに沿ったものが多いです。
というのも、検定の手順自体が決まっているので、仮説を設定し、検定統計量を求めて、有意性を判定する流れは常に同じであるためです。
片側検定と両側検定、検定統計量の符号を混同しがちですが、気を付けるポイントは限られているので、あらかじめ意識しておけばケアレスミスも減らせます。


実験計画法
- 分散分析表を計算して埋める問題
- 因子の最適組合せを選び、母平均の点推定を求める問題
- 有効反復数と信頼区間を求める問題
- 実験計画法の定義に関する用語を選ぶ問題
問題を見るだけで圧倒されそうな難しそうな雰囲気が漂っていますが、実は実験計画法も解法の流れがおおむね決まっています。
基本的には、分散分析表を作成してF検定で有意性を判定するだけなので、計算方法さえ理解していれば、あとはひたすら電卓を叩いて計算すれば問題ありません。
ただ、その反面として、最初の平方和の計算で間違えると残りの小問も道連れとなり、正しい答えを導けなくなってしまうので、特に注意が必要です。
また、因子の最適組合せから点推定を求めるところまでは、確実に得点できるように備えておきたいところですが、問題の終盤に登場する信頼区間は少々厄介です。
交互作用が有意か否かで計算方法が異なりますし、さらには有効反復数という概念まで登場するので、各段に難易度が上がったように思えます。
もちろん余力があればすべて解くことが望ましいですが、あくまで正答率7割程度が合格の目安なので、時間との都合を見ながら、思い切って飛ばす決断をすることも大事です。


抜取検査
- 生産者危険/消費者危険、ロット合格/不合格の定義の問題
- 抜取検査表からサンプルの大きさと合格判定値を読む問題
- OC曲線の形状を選ぶ問題
計数規準型も計量規準型も2級の問題では付表の抜取検査表を読み取る程度なので、思ったほど専門性の高い解法を求められる内容ではありません。
付表の縦軸と横軸の交差する箇所を読み取るだけなので、極端な話、予備知識がほとんどなくても、直感的に数値を当てはめてみれば、案外と正解を導けることもあるかもしれません。
しかし、抜取検査では専門用語が多く登場するので、あらかじめ定義をきちんと理解しておかないと、問題文がサッパリ理解できないかもしれないので、油断は禁物です。
また、OC曲線(検査特性曲線)も難解そうに見える要因の一つですが、これも考え方は意外とシンプルです。
特に、サンプルサイズや合格判定個数を変えた場合のOC曲線の変化を問われる問題では、問題文の意味を理解できないと、思い切って二択で勝負する方もいるかもしれません。
ただ、簡単に言うと、検査が緩くなるのか厳しくなるのかというだけの話なので、OC曲線のグラフの構成をきちんと理解しておけば、過剰に心配する必要はありません。


信頼性工学
- 信頼性システムの信頼度を計算する問題
- 信頼度が最も高く(または低く)なる配置を選ぶ問題
- システムの名称を選ぶ問題
信頼性工学というと、非常に幅広い専門知識を問われているように思いがちですが、2級の出題内容としては、その入り口の割と単純な問題が多いです。
具体的には信頼度を求める問題で、部品を直列か並列の組合せでシステムを構成し、部品ごとの信頼度からシステム全体の信頼度を計算する内容です。
要素としては直列か並列の2通りしかないので、それぞれの計算のしかたさえ覚えておけば、簡単な計算だけで対処できます。

まとめ
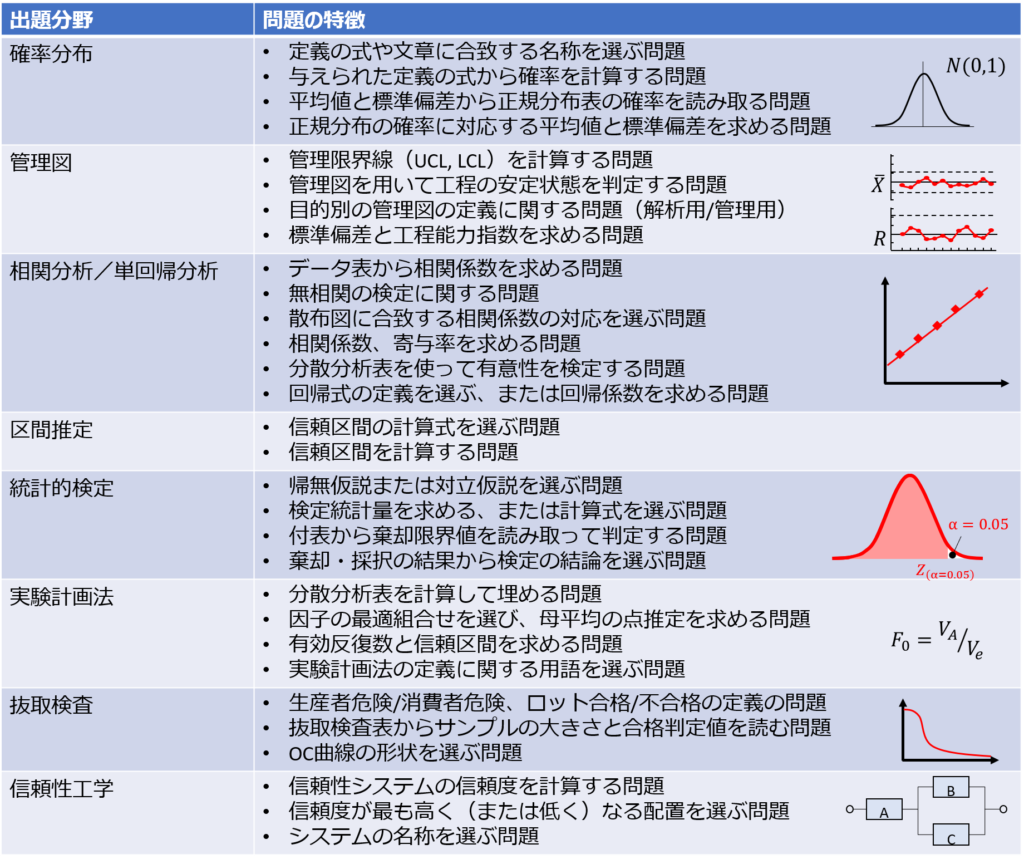
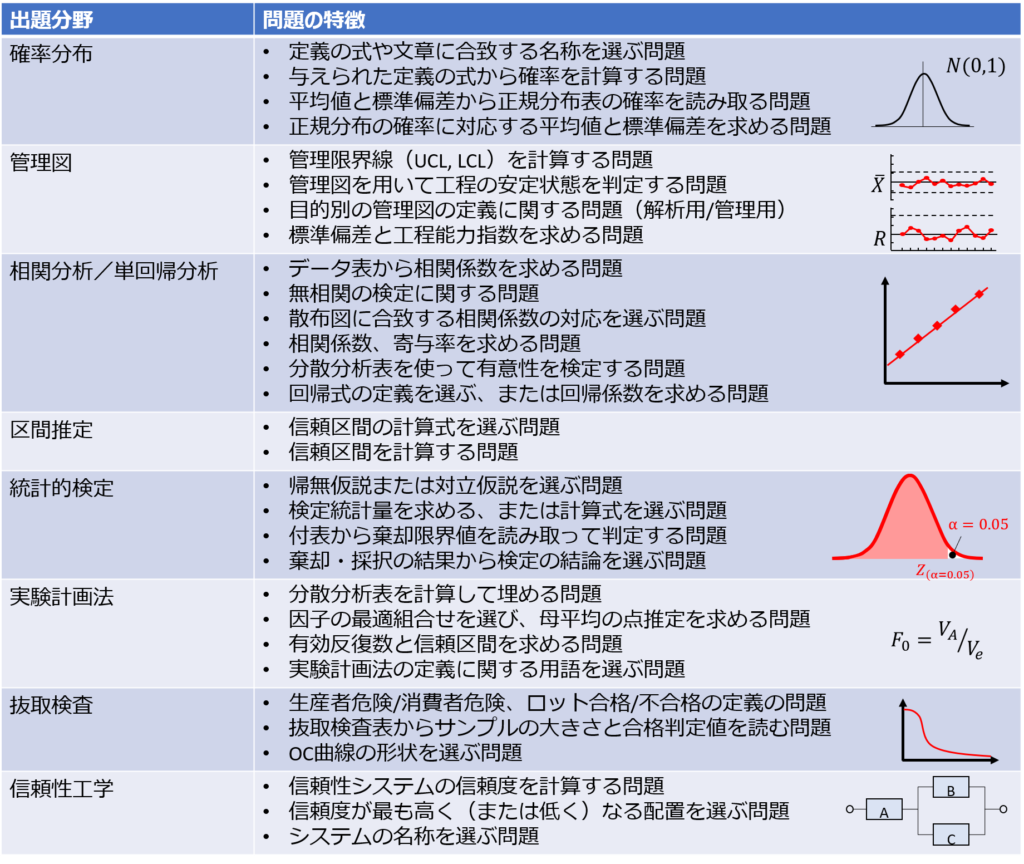
最後に出題分野と問題の特徴をもう一度整理しておきます。
なお、QC検定のおすすめ勉強方法や教材については、以下の記事で詳しく紹介していますので、合わせてご覧ください。

それでは、皆さまのご健闘をお祈りしております。





コメント